Huffman-Code Implementierung (C++): Cpp String-Compression
11.06.2012
In den letzten Tagen habe ich für einen Vortrag den Huffman Algorithmus in Cpp implementiert.
Da ich das Thema der String-Kompression sehr interessant finde, will ich euch heute den Code und die verschiedenen algorithmischen Herangehensweisen dazu vorstellen.
Zum Überblick aber erst mal ein paar Daten des Projekts:
Die Huffman-Klasse selbst, stellt alle notwendigen Möglichkeiten zur Verfügung, die der Huffman-Algorithmus ermöglicht.
Er ist stark an den Shannon-Fano-Algorithmus angelehnt. Allerdings ist die Optimalität des Binärbaums garantiert (Beweis siehe: Wikipedia-Artikel)
Dort sind auch weitere Beschreibungen zur theoretischen Funktionsweise nachzulesen. Auf diese möchte ich nicht länger eingehen, sondern mich auf die Implementierung konzentrieren. Eine Präsentation von mir auf Englisch über die theoretischen Ansätze, Vor- und Nachteile des Huffman Codes findet ihr aber auch in meiner Filebase.
Jetzt aber zu den Funktionen, die in diesem Projekt am Ende zur Verfügung stehen. Hierbei habe ich neben den notwendigen reinen Kompressionen und Dekompressionen auch die Möglichkeit eingebaut, dies über ganze Dateien zu erledigen.
Außerdem besteht die Möglichkeit zwischen verschiedenen Implementierungen der Kompression auszuwählen (3 an der Zahl).
Als kleinen Schmankerl habe ich eine Option eingebaut, sich den Binärbaum selbst anzusehen. Dies greift auf Graphviz zu, was dazu installiert sein muss. Der Binär-Baum wird hierzu von meinem Programm formatiert in eine Text-Datei gespeichert. Anschließend wird die dot.exe, die aus dem bin-Ordner von Graphviz in den data Ordner meines Programms kopiert werden sollte, für diese erstellte Textdatei aufgerufen.
Das ganze ist derzeit auf ASCII ausgelegt, kann aber ohne weiteres erweitert werden. Hierzu sind nur wenige Änderungen notwendig.
Das Projekt besteht insgesamt aus 4 Klassen und der Main-Datei. Hierbei sind aber nur 2-3 von größerem Interesse.
Die anderen werde ich nur kurz vorstellen und nicht viel mehr darauf eingehen.
Eine kurze Übersicht:
main.h & main.cpp: Benutzerabfragen etc. zum Navigieren durch das Programm
menu.h & menu.cpp: Bereitstellung eines allgemeinen formatierten Menüs
letter.h & letter.cpp: Nur zum Erstellen des Binärbaums genutzt, um die vorkommenden Buchstaben und deren Häufigkeit festzuhalten.
huffmanElement.h & huffmanElement.cpp: Hier werden die einzelnen Knoten und Blätter des Binärbaums gespeichert. Hinzu kommen verschiedene Daten, die zur Realisierung des jeweilig gewählten Kompressions-Algorithmus benötigt werden.
huffman.h & huffman.cpp: Enthalten ist ein Algorithmus zum Erstellen des nachweislich perfekten Binärbaums, einer zum Dekomprimieren der Daten und 3 verschiedene zum Komprimieren.
Eine mit Doxygen erzeugte Dokumentation ist hier zu finden: Huffman-Code-Dokumentation
Ich möchte euch zuerst die Codes der main.h, main.cpp, menu.h und menu.cpp zeigen. Dazu ist nicht mehr zu sagen, als dass in der main ein Objekt der Huffman-Klasse auf dem Heap erzeugt wird und auf dieses bei verschiedenen Menüauswahlen die jeweilige Methode des Huffman-Objekts aufgerufen. Abschließend wird das Objekt ordnungsgemäß vom Speicher entfernt. Gleiches gilt natürlich auch für die Speicherbereiche der Objekte der anderen Klassen. Darauf will ich im Folgenden nicht weiter eingehen (die Destruktoren, Kopierkonstruktoren etc. haben nichts mit dem Algorithmus als solchem zu tun und werden daher nicht weiter erklärt).
main.h
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | #ifndef MAIN_HEADER #define MAIN_HEADER #include <iostream> #include <fstream> #include <vector> #include <ctime> #include "menu.h" #include "huffman.h" using namespace std; string read_string(); string read_filename(bool exist); vector<bool> compress_single(Huffman* huffman_compr); void decompress_single(Huffman* huffman_compr, vector<bool> compr_bits); bool* compress_file(Huffman* huffman_compr, bool* compr_bits, int* count, int algo_id); void save_compression(bool* compr_bits, int length); void save_decompression(Huffman* huffman_compr); void build_tree(Huffman* huffman_compr, string filename); #endif |
main.cpp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 | /** @file main.cpp Datei zum Starten eines Menues und Ausfuehren des Huffman-Algorithmus @author - David Hadizadeh @version - 1.0 @date - 07.06.2012 */ #include "main.h" /** Start-Funktion, die ein Objekt der Huffman-Klasse auf dem Heap erzeugt und auf dieses bei verschiedenen Menüauswahlen die jeweilige Methode des Huffman-Objekts aufruft. Abschliessend wird das Objekt ordnungsgemaess vom Speicher entfernt. @param argc Anzahl uebergebener Parameter @param argv Parameter-Feld, das beim Start des Programms uebergeben wird @returns Wert der angibt, ob das Programm korrekt beendet wurde (0 = korrekt). */ int main(int argc, char *argv[]) { Huffman* huffman_compr = new Huffman(); vector<bool> cur_compression; build_tree(huffman_compr, "data/english"); bool* compr_bits = 0; int count_bits = 0; const int COUNT_MENU = 8; const string MENU_NAMES[COUNT_MENU] = { "Aktuellen Huffman-Tree anzeigen", "Neuen Huffman-Tree anhand einer Textdatei generieren.", "Manuellen Text komprimieren und ausgeben", "Manuell eingegebenen komprimierten Text dekomprimiert ausgeben", "Datei komprimieren und abspeichern [intuitiver Algorithmus]", "Datei komprimieren und abspeichern [mit einfacher Tabelle]", "Datei komprimieren und abspeichern [mit Hash-Look-Up Tabelle]", "Komprimierte Datei dekomprimieren und als Datei speichern", }; int selection = COUNT_MENU; do { cout << "Bitte waehlen Sie einen Menuepunkt aus:" << endl << endl; selection = get_menu(MENU_NAMES, COUNT_MENU); switch(selection) { case 1: system("data\\tree.png"); break; case 2: build_tree(huffman_compr, read_filename(true)); break; case 3: cur_compression = compress_single(huffman_compr); break; case 4: decompress_single(huffman_compr, cur_compression); break; case 5: compr_bits = compress_file(huffman_compr, compr_bits, &count_bits, 0); save_compression(compr_bits, count_bits); break; case 6: compr_bits = compress_file(huffman_compr, compr_bits, &count_bits, 1); save_compression(compr_bits, count_bits); break; case 7: compr_bits = compress_file(huffman_compr, compr_bits, &count_bits, 2); save_compression(compr_bits, count_bits); break; case 8: save_decompression(huffman_compr); break; } cout << endl << endl; } while(selection != (COUNT_MENU + 1)); delete huffman_compr; return 0; } /** Liest einen Text (mit Leerzeichen) ein und leert vor- und nachher den Puffer. @returns eingelesenen Text */ string read_string() { string text = ""; cin.seekg(0, std::ios::end); cin.clear(); getline(cin, text); cin.seekg(0, std::ios::end); cin.clear(); return text; } /** Fragt nach einem Dateinamen, liest ihn ein und prueft, ob die Datei existiert. Je nach Parameteruebergabe wird dies so lange wiederholt, wie erforderlich. @param exist 0, wenn die Datei nicht existieren muss, sonst muss sie existieren @returns eingelesener Dateiname */ string read_filename(bool exist) { string filename; do { cout << "Bitte geben Sie einen Dateinamen ein: "; filename = read_string(); ifstream check_file("data/" + filename); if(exist && !check_file) { cout << "Diese Datei existiert nicht." << endl; filename = ""; } else { filename = "data/" + filename; } } while (filename == "" && exist); return filename; } /** Komprimiert einen einzelnen einzulesenden Text und gibt deren Kompressionsbits aus. @param huffman_compr Zeiger auf ein Huffman-Objekt, das zum Ausfuehren des Algorithmus verwendet wird @returns Kompressions-Bits */ vector<bool> compress_single(Huffman* huffman_compr) { string text; vector<bool> compr_bits_vec; cout << "Bitte geben Sie den Text ein, der komprimiert werden soll:" << endl; text = read_string(); bool* compr_bits = 0; int count_compr_bits = 0; //compr_bits = huffman_compr->compress_lookup(compr_bits, &count_compr_bits, text, false); compr_bits = huffman_compr->compress_table(compr_bits, &count_compr_bits, text, false); cout << endl << "Komprimierter Text: " << endl; for (unsigned int i = 0; i < count_compr_bits; i++) { compr_bits_vec.push_back(compr_bits[i]); cout << compr_bits[i]; } cout << endl << endl; if (compr_bits != 0) { delete [] compr_bits; compr_bits = 0; } return compr_bits_vec; } /** Dekomprimiert uebergebene Bits mit dem Huffman-Algorithmus und gibt den dekomprimierten Text aus. @param huffman_compr Zeiger auf ein Huffman-Objekt, das zum Ausfuehren des Algorithmus verwendet wird @param compr_bits text */ void decompress_single(Huffman* huffman_compr, vector<bool> compr_bits) { string read_string; cout << "Der derzeit gespeicherte komprimierte Bitstream ist dekomprimiert:" << endl; cout << huffman_compr->decompress(compr_bits) << endl << endl; } /** Komprimiert eine komplette Datei auf 3 verschiedene Arten und gibt deren Dauer aus. @param huffman_compr Zeiger auf ein Huffman-Objekt, das zum Ausfuehren des Algorithmus verwendet wird @param algo_id Algorithmus-ID, 0 fuer intuitiven, 1 fuer tabellearischen, sonst Loookup Algorithmus @returns Zeiger auf Komprimierte Bits */ bool* compress_file(Huffman* huffman_compr, bool* compr_bits, int* count, int algo_id) { cout << "Zu komprimierende Datei:" << endl; string compr_file = read_filename(true); clock_t time_start = clock(); if (algo_id == 0) { compr_bits = huffman_compr->compress(compr_bits, count, compr_file, true); } else if (algo_id == 1) { compr_bits = huffman_compr->compress_table(compr_bits, count, compr_file, true); } else { compr_bits = huffman_compr->compress_lookup(compr_bits, count, compr_file, true); } cout << endl << "Dauer: " << ((double)(clock() - time_start)) / 1000.0 << " Sekunden" << endl << endl; return compr_bits; } /** Speichert die uebergebenen Bits in einer Datei. @param compr_bits zu speichernde Bits */ void save_compression(bool* compr_bits, int length) { cout << "Ausgabe-Datei:" << endl; char value = 0; int j = 0; fstream f; f.open(read_filename(false), ios::out); for (int i = 0; i < length; i++) { value |= compr_bits[i] << (j % 8); j++; if (j % 8 == 0) { f << value; value = 0; } } if (j % 8 != 0) { f << value; } f.close(); if (compr_bits != 0) { delete [] compr_bits; compr_bits = 0; } } /** Liest eine komprimierte Datei ein, dekomprimiert sie und speichert sie in einer anderen Datei. Die Dateinamen werden jeweils eingelesen. @param huffman_compr Zeiger auf ein Huffman-Objekt, das zum Ausfuehren des Algorithmus verwendet wird */ void save_decompression(Huffman* huffman_compr) { cout << "Einlese-Datei:" << endl; string filename = read_filename(true); cout << "Ausgabe-Datei:" << endl; huffman_compr->decompress(filename, read_filename(false)); } /** Erzeugt einen Huffman-Binaer-Baum anhand einer Datei. @param huffman_compr Zeiger auf ein Huffman-Objekt, das zum Ausfuehren des Algorithmus verwendet wird @param filename Dateiname der Datei, die als Wortvorlage verwendet wird */ void build_tree(Huffman* huffman_compr, string filename) { huffman_compr->build_tree(filename, true); huffman_compr->save_tree("data/tree.txt"); system("data\\dot.exe -Tpng data/tree.txt > data/tree.png"); } |
menu.h
1 2 3 4 5 6 7 8 9 10 11 12 13 | #ifndef MENU_HEADER #define MENU_HEADER #include <iostream> #include <sstream> using namespace std; void print_menu_names(const string names[], int count); int get_menu(const string names[], int count); #endif |
menu.cpp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 | /** @file menu.cpp Liefert Funktionalitaet, um ein Menue auszugeben und aus diesem Menue die einzelnen Punkte mit Zahlen auszuwaehlen. @author - David Hadizadeh @version - 1.0 @date - 07.06.2012 */ #include <iostream> #include <iomanip> #include <cstring> #include <sstream> #include "menu.h" using namespace std; /** Gibt das Menue mit uebergebenen Punkten geordnet und nummeriert aus. Der Menue-Punkt Programm-Beenden wird automatisch erzeugt. @param names Feld mit Namen der Menue-Punkte @param count Anzahl der Menue-Punkte */ void print_menu_names(const string names[], int count) { int x = 0; for(x = 0; x < count; x++) { std::ostringstream stm; stm << "(" << (x+1) << ")"; cout << left << setw(6) << stm.str(); cout << names[x] << endl; } cout << setw(0) << "(" << (x+1) << ") "; if (x+1 > 9) { cout << "Beenden"; } else { cout << " Beenden"; } cout << endl << endl; } /** Ruft das Ausgeben des Menues auf und erfasst die Benutzereingabe zum waehlen eines Menue-Punktes. @param names Feld mit Namen der Menue-Punkte @param count Anzahl der Menue-Punkte @returns ausgewaehlte Menue-Punkt-Nummer */ int get_menu(const string names[], int count) { cout << "Bitte waehlen:" << endl; print_menu_names(names, count); int result = 0; cout << "Bitte geben Sie einen Menuepunkt ein: "; cin.seekg(0, std::ios::end); cin.clear(); cin >> result; cin.seekg(0, std::ios::end); cin.clear(); cout << endl << endl; return result; } |
Das war also das Grundgerüst des Programms.
Kommen wir nun zum eigentlich interessanten Teil:
Fangen wir mit der Letter-Klasse an. Sie wird genutzt, um beim Einlesen der Binär-Baum-Vorlagedatei die jeweiligen Buchstaben mit deren Vorkommnis-Anzahlen zu speichern und bei der Sortierung der Blätter abzufragen.
Die Überladung des < Operators ist notwendig, um die Buchstaben bei der Sortierung vergleichen zu können (nicht der Buchstabe selbst zählt, sondern dessen Vorkommnise). Dieser < Operator wird von der Funktion sort (algorithm) in der Huffman-Klasse verwendet.
letter.h
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | #ifndef LETTER_HEADER #define LETTER_HEADER /** Klasse zum Verwalten von Buchstaben und deren Anzahlen */ class Letter { private: /** Buchstabe */ int letter; /** Anzahl an Vorkommnissen des Buchstabens */ int count; public: Letter(); Letter(int cur_letter); virtual bool operator< (const Letter& compare) const; virtual int get_letter() const; virtual int get_count() const; virtual void add_count(); private: }; #endif |
letter.cpp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | /** @file letter.cpp Verwalten von Buchstaben und deren Anzahlen @author - David Hadizadeh @version - 1.0 @date - 07.06.2012 */ #include "letter.h" /** Erzeugt einen Buchstaben mit 0 als Wert und 0 als Vorkommens-Anzahl */ Letter::Letter() { letter = 0; count = 0; } /** Erzeugt einen Buchstaben mit 0 als Vorkommens-Anzahl @param cur_letter Dezimalwert des Buchstaben */ Letter::Letter(int cur_letter) { letter = cur_letter; count = 0; } /** Ueberladung des < Operator ermoeglicht den Vergleich von Buchstaben. Buchstaben mit geringerer Anzahl sind kleiner als Buchstaben mit groesserer Vorkommens-Anzahl. @param compare zu vergleichender Buchstabe @returns 0, wenn der aktuelle Buchstabe nicht kleiner ist, sonst ist er kleiner */ bool Letter::operator< (const Letter& compare) const { return (count < compare.get_count()); } /** Liefert den aktuellen Buchstaben. @returns aktueller Buchstabe */ int Letter::get_letter() const { return letter; } /** Liefert die aktuelle Vorkommens-Anzahl. @returns Anzahl */ int Letter::get_count() const { return count; } /** Erhoeht die Vorkommens-Anzahl um 1. */ void Letter::add_count() { count++; } |
Weiter geht es mit der HuffmanElement-Klasse. Sie dient der Speicherung der Knoten und Blätter des Binär-Baums.
In jedem Knoten/Blatt werden zusätzlich der linke und der rechte Nachfolger gespeichert. Somit ist die Verknüpfen zwischen den Knoten sicher gestellt. Für die Knoten werden außerdem Namen gespeichert (zur Darstellung des Baums), für die Blätter werden die jeweiligen Buchstaben/Zeichen gespeichert. Um die verschiedenen Algorithmen zu realisieren, sind außerdem weitere Informationen notwendig. Diese werden nicht von allen der 3 Algorithmen verwendet, müssen aber für die anderen bereit gestellt werden. Zum einen wird der Vorgänger-Knoten zum anderen auch die aktuelle Seite (rechts oder links vom Vorgänger) festgesetzt. Für den Lookup-Algorithmus werden außerdem die Codes für jedes Blatt gesichert. Somit muss der Baum später nicht mehr durchlaufen werden. Stattdessen kann über die gesicherten Lookup-Codes komprimiert werden. Auch wird eine Vergleichsfunktion für HuffmanElement-Objekte bereit gestellt. Diese ist zum absteigenden Sortieren der Blätter/Knoten vorgesehen.
huffmanElement.h
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 | #ifndef HUFFMAN_ELEMENT_HEADER #define HUFFMAN_ELEMENT_HEADER #include <list> using namespace std; /** Klasse zum Verwalten von Huffman-Knoten und -Blaettern */ class HuffmanElement { private: /** Anzahl der Gesamtknoten */ static int count_nodes; /** Groesse des laengsten Lookup-Codes */ static int longest_code; /** Name des Knotens */ int name; /** Buchstabe des Blatts */ char letter; /** Linker Ast */ HuffmanElement* left; /** Rechter Ast */ HuffmanElement* right; /** Wert des Asts */ int value; /** Uebergeordneter Knoten */ HuffmanElement* parent; /** Ist es ein rechter Ast, dann true, sonst ist es ein linker Ast */ bool is_right; /** Binaer-Code des Knotens/Blatts */ bool* lookup_code; /** Laenge des Binaer-Codes des Knotens/Blatts */ unsigned int lookup_code_length; public: HuffmanElement(); HuffmanElement(char cur_letter, int cur_value); HuffmanElement(HuffmanElement* cur_left, HuffmanElement* cur_right, int cur_value); HuffmanElement(const HuffmanElement& original); virtual ~HuffmanElement(); virtual HuffmanElement& operator=(const HuffmanElement& original); virtual bool operator> (const HuffmanElement& compare) const; virtual char get_letter() const; virtual int get_value() const; virtual int get_name() const; virtual bool get_is_right() const; virtual HuffmanElement* get_parent(); virtual HuffmanElement* get_left(); virtual HuffmanElement* get_right(); virtual bool* get_lookup_code(); virtual unsigned int get_lookup_code_length() const; virtual void set_parent(HuffmanElement* cur_parent, bool cur_is_right); virtual void add_lookup_code(bool code); virtual int get_longest_code(); private: void copy_huffman_element(const HuffmanElement& original); void delete_huffman_element(); }; /** Comparator zum Vergleichen von Knoten/Blaettern */ struct compareCharacters { bool operator ()(HuffmanElement *left, HuffmanElement *right) { return *left > *right; } }; #endif |
huffmanElement.cpp
/** @file huffmanElement.cpp Verwalten von Huffman-Knoten und -Blaettern @author - David Hadizadeh @version - 1.0 @date - 07.06.2012 */ #include "huffmanElement.h" int HuffmanElement::count_nodes = 1; int HuffmanElement::longest_code = 0; /** Erzeugt einen leeren Knoten. Reserviert Speicher fuer 30 Lookup-Bits. */ HuffmanElement::HuffmanElement() { left = 0; right = 0; parent = 0; name = 0; letter = -1; value = 0; is_right = false; lookup_code = new bool[30]; lookup_code_length = 0; } /** Erzeugt ein Blatt mit Buchstaben und deren Anzahl. Reserviert Speicher fuer 30 Lookup-Bits. @param cur_letter Buchstabe @param cur_value Anzahl */ HuffmanElement::HuffmanElement(char cur_letter, int cur_value) : letter(cur_letter), value(cur_value) { left = 0; right = 0; name = 0; is_right = false; parent = 0; lookup_code = new bool[30]; lookup_code_length = 0; } /** Erzeugt einen Knoten mit linkem und rechtem Nachfolger, sowie einem Wert, der die Wertigkeit des aktuellen Asts angibt. Reserviert Speicher fuer 30 Lookup-Bits. @param cur_left linker Nachfolger @param cur_right rechter Nachfolger @param cur_value Wert des Asts */ HuffmanElement::HuffmanElement(HuffmanElement* cur_left, HuffmanElement* cur_right, int cur_value) : left(cur_left), right(cur_right), value(cur_value) { letter = -1; name = count_nodes; count_nodes++; is_right = false; parent = 0; lookup_code = new bool[30]; lookup_code_length = 0; } /** Kopiert einen Knoten/Blatt. @param original zu kopierender Knoten/Blatt */ HuffmanElement::HuffmanElement(const HuffmanElement& original) { copy_huffman_element(original); } /** Gibt alle Speicherbereiche des Knotens/Blatt frei. */ HuffmanElement::~HuffmanElement() { delete_huffman_element(); } /** Zuweisungsoperator zum Kopieren/Zuweisen eines Kontens/Blatts. @param original zuzuweisender Knoten/Blatt @returns Referenz auf den neuen Knoten/Blatt */ HuffmanElement& HuffmanElement::operator=(const HuffmanElement& original) { copy_huffman_element(original); return *this; } /** Ueberladung des > Operator ermoeglicht den Vergleich von Knoten/Blaettern. Knoten/Blaettern mit grossem Wert sind groesser als Knoten/Blaettern mit kleinem Wert. @param compare zu vergleichender Knoten @returns 0, wenn der aktuelle Knoten nicht groesser ist, sonst ist er groesser */ bool HuffmanElement::operator> (const HuffmanElement& compare) const { return (value > compare.get_value()); } /** Liefert den aktuellen Buchstaben. @returns Buchstabe */ char HuffmanElement::get_letter() const { return letter; } /** Liefert den aktuellen Wert (Wertigkeit des aktuellen Asts) @returns Wertigkeit */ int HuffmanElement::get_value() const { return value; } /** Liefert den Namen des Knotens (Nummer) @returns Namens-ID */ int HuffmanElement::get_name() const { return name; } /** Gibt an, ob der aktuelle Knoten/Blatt ein rechter oder linker Nachfolger ist. @returns 0, wenn es ein liker Nachfolger ist, sonst ist es ein rechter Nachfolger */ bool HuffmanElement::get_is_right() const { return is_right; } /** Liefert den uebergeordneten Knoten. @returns uebergeordneter Knoten */ HuffmanElement* HuffmanElement::get_parent() { return parent; } /** Liefert den linken Nachfolger. @returns linker Nachfolger */ HuffmanElement* HuffmanElement::get_left() { return left; } /** Liefert den rechten Nachfolger. @returns rechter Nachfolger */ HuffmanElement* HuffmanElement::get_right() { return right; } /** Liefert den Lookup-Code des aktuellen Blatts. @returns Lookup-Bit-Code */ bool* HuffmanElement::get_lookup_code() { return lookup_code; } /** Liefert die Laenge des Lookup-Codes des aktuellen Blatts. @returns Laenge des Lookup-Bit-Codes */ unsigned int HuffmanElement::get_lookup_code_length() const { return lookup_code_length; } /** Legt den Uebergeordneten Knoten fest und bestimmt, ob der aktuelle Knoten/Blatt ein linker oder rechter ist. @param cur_parent uebergeordneter Knoten @param cur_is_right 0, wenn es ein liker Nachfolger ist, sonst ist es ein rechter Nachfolger */ void HuffmanElement::set_parent(HuffmanElement* cur_parent, bool cur_is_right) { parent = cur_parent; is_right = cur_is_right; add_lookup_code(cur_is_right); } /** Fuegt ein uebergebenes Bit zum eigenen Lookup-Code hinzu und macht dies auch fuer alle Nachfolger des aktuellen Knotens. @param code hinzuzufuegendes Bit */ void HuffmanElement::add_lookup_code(bool code) { lookup_code[lookup_code_length] = code; ++lookup_code_length; //lookup_code.push_front(code); if (longest_code < lookup_code_length) { longest_code = lookup_code_length; } if (left != 0) { left->add_lookup_code(code); } if (right != 0) { right->add_lookup_code(code); } } /** Liefert die Laenge des laengsten Lookup-Codes. @returns Anzahl an Stellen des laengsten Lookup-Codes */ int HuffmanElement::get_longest_code() { return longest_code; } /** Kopiert einen Knoten/Blatt. @param original zu kopierender Knoten/Blatt */ void HuffmanElement::copy_huffman_element(const HuffmanElement& original) { if (this != &original) { delete_huffman_element(); left = original.left; right = original.right; parent = original.parent; name = original.name; letter = original.letter; value = original.value; is_right = original.is_right; lookup_code = original.lookup_code; } } /** Gibt alle Speicherbereiche des aktuellen Knotens frei. */ void HuffmanElement::delete_huffman_element() { if (left != 0) { delete left; } if (right != 0) { delete right; } if (lookup_code != 0) { delete [] lookup_code; } } |
Kommen wir nun abschließend zur Haupt-Klasse: Die Huffman-Klasse.
Diese will ich etwas aufgeschlüsselter präsentieren. Zuerst allerdings die Header-Datei:
huffman.h
#ifndef HUFFMAN_HEADER #define HUFFMAN_HEADER #include <iostream> #include <sstream> #include <fstream> #include <vector> #include <list> #include <algorithm> #include <ctime> #include "huffmanElement.h" #include "letter.h" using namespace std; /** Ermoeglicht das Erstellen eines Huffman-Binaer-Baums, deren Speicherung und Loeschung. Ausserdem die Kompression auf 3 verschiedene Arten und die Dekompression. Jeweils von Strings oder von ganzen Dateien. */ class Huffman { private: /** Anzahl an maximalen Buchstaben des Binaer-Baums */ static const int ENCODING_MAX; /** Blaetter des Baums */ vector<HuffmanElement*> tree; /** Oberster Knoten des Binaerbaums */ HuffmanElement* root; /** Look-Up-Struktur zum Speichern und Lesen von Blatt-Positionen */ int* lookup_positions; /** Zaehlt Anzahnl der Statusmeldungen */ int print_status_counter; public: Huffman(); Huffman(const Huffman& original); virtual ~Huffman(); virtual Huffman& operator=(const Huffman& original); virtual void build_tree(string text, bool file); virtual bool* compress(bool* compr_bits_ar, int* count, string text, bool file); virtual bool* compress_table(bool* compr_bits_ar, int* count, string text, bool file); virtual bool* compress_lookup(bool* compr_bits_ar, int* count, string text, bool file); virtual void decompress(string filename, string out_filename); virtual string decompress(vector<bool> compr_bits); virtual void save_tree(string filename) const; private: void copy_huffman(const Huffman& original); void delete_huffman(); string decompress(bool* compr_bits, int count, string filename); void save_element(fstream* f, HuffmanElement* element) const; bool depth_search(char search_node, HuffmanElement* node, vector<bool>* compr_buffer); void read_file(string filename, vector<Letter>* letters) const; void read_file(string filename, vector<char>* letters) const; string to_ascii(string text) const; void print_and_write(string file_name, string text) const; int insert_compr_bits(bool* compr_bits, unsigned int compr_bits_index, bool* compr_bits_rev, HuffmanElement* cur_element) const; void print_status(int overall, int current); }; #endif |
Die Implementierung dieser Klasse besteht im Grunde aus den 3 Algorithmen zur Kompression, dem zur Dekompression und dem Erstellen des Baumes. Die weiteren Funktionen sind nicht zwingend für den Huffman-Code notwendig, sind aber in meinen Augen eine schöne Erweiterung.
Fangen wir von vorne an, nach dem includen der Header-Datei ist zuerst das Klassen-Attribut ENCODING_MAX zu setzen.
Dieser legt im Groben fest, welche Buchstaben der Algorithmus kennen und auflösen kann. Dies habe ich in dem Fall auf 127 (ASCII) gesetzt.
Zum Konstruktor, Destruktor, Kopierkonstruktor und Zuweisungsoperator:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | /** Erzeugt einen Huffman-Verwalter. */ Huffman::Huffman() { print_status_counter = 0; lookup_positions = 0; root = 0; } /** Kopiert einen Huffman-Verwalter. @param original zu kopierender Huffman-Verwalter */ Huffman::Huffman(const Huffman& original) { copy_huffman(original); } /** Loescht einen Huffman-Verwalter. */ Huffman::~Huffman() { delete_huffman(); } /** Zuweisungsoperator fuer einen Huffman-Verwalter. @param original zuzuweisender Huffman-Verwalter @returns Referenz auf zugewiesenen Huffman-Verwalter */ Huffman& Huffman::operator=(const Huffman& original) { copy_huffman(original); return *this; } |
Manch einer fragt sich vielleicht, wozu diese nun alle notwendig sind, da sie in meinem Programm nicht alle Verwendung finden (nur der Konstruktor und Destruktor). Da aber der Destruktor implementiert wurde, befolge ich die „Rule of three“. Diese besagt, dass bei C++ alle 3 genannten Elemente zu schreiben sind, wenn man eines davon verwendet.
Nach diesen Grundelementen geht es weiter mit dem Erstellen des Binär-Baums.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | /** Erzeugt einen Huffman-Binaer-Baum anhand einer Datei oder eines uebergebenen Textes. Der Baum ist fuer die Komprimierung optimal. @param text Dateiname/Text @param file 0, wenn der Baum aus einem Text erzeugt werden soll, sonst aus einer Datei */ void Huffman::build_tree(string text, bool file) { delete_huffman(); tree.clear(); vector tmp_tree; vector letters; for (unsigned int i = 0; i < ENCODING_MAX; i++) { letters.push_back(Letter(i)); } if (file) { read_file(text, &letters); } else { for (unsigned int i = 0; i < text.length(); i++) { letters.at(text[i]).add_count(); } } sort(letters.begin(), letters.end()); lookup_positions = new int[ENCODING_MAX]; for (unsigned int i = ENCODING_MAX - 1; i >= 0 && letters[i].get_count() > 0; i--) { tmp_tree.push_back(new HuffmanElement(letters[i].get_letter(), letters[i].get_count())); tree.push_back(tmp_tree[tmp_tree.size()-1]); lookup_positions[letters[i].get_letter()] = tree.size()-1; } |
Im ersten Teil der Methode werden entweder aus einer Datei oder aus einem übergebenen Text alle Buchstaben und deren Häufigkeit ausgelesen und gespeichert. Anschließend werden die Buchstaben, die mindestens ein Mal vorkamen, in einen Vektor mit Zeigern auf alle Blätter gelegt.
1 2 3 4 5 6 7 8 9 10 | while (tmp_tree.size() > 1) { tmp_tree.push_back(new HuffmanElement(tmp_tree[tmp_tree.size()-1], tmp_tree[tmp_tree.size()-2], tmp_tree[tmp_tree.size()-1]->get_value() + tmp_tree[tmp_tree.size()-2]->get_value())); root = tmp_tree[tmp_tree.size()-1]; tmp_tree[tmp_tree.size()-2]->set_parent(root, false); tmp_tree[tmp_tree.size()-3]->set_parent(root, true); tmp_tree.erase(remove(tmp_tree.begin(), tmp_tree.end(), tmp_tree[tmp_tree.size()-2]), tmp_tree.end()); tmp_tree.erase(remove(tmp_tree.begin(), tmp_tree.end(), tmp_tree[tmp_tree.size()-2]), tmp_tree.end()); sort(tmp_tree.begin(), tmp_tree.end(), compareCharacters()); } } |
Nun beginnt die Baumerzeugung. Solange es mehr als einen Hauptknoten gibt, werden die beiden Äste mit der kleinsten Wertigkeit (Vorkommnisse) aus dem Vektor entfernt und einem neuen Knoten, der dem Vektor hinzugefügt wird, untergeordnet. Abschließend wird der Vektor wieder sortiert, um im nächsten Schritt wieder die Äste mit der kleinsten Wertigkeit am Ende des Vektors vorfinden zu können.
Der Vektor wird anschließend nicht mehr benötigt, da wir nur einen Zeiger auf den Root-Knoten benötigen, der als Attribut abgespeichert ist.
Als nächstes geht es zu den Kompressionen, wobei ich hier mit der intuitiven Methode beginne.
Diese läuft den jeweiligen Text Zeichen für Zeichen durch und durchsucht für jedes Zeichen den gesamten Baum per Tiefensuche.
Meine rekursive Tiefensuche:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | /** Rekursive Tiefensuche. Durchsucht den Binaerbaum nach einem uebergebenen Blatt und speichert die Bits, die zum Erreichen notwendig waren. @param search_node zu suchendes Blatt @param node aktuelles Blatt @param compr_buffer derzeit gespeicherte Bitfolge @returns 0, wenn Blatt nicht gefunden wurde, sonst wurde es gefunden */ bool Huffman::depth_search(char search_node, HuffmanElement* node, vector* compr_buffer) { bool success = false; if (node->get_left() != 0 || node->get_right() != 0) { if (node->get_left() != 0) { compr_buffer->push_back(false); success = depth_search(search_node, node->get_left(), compr_buffer); } if (!success && node->get_right() != 0) { compr_buffer->push_back(true); success = depth_search(search_node, node->get_right(), compr_buffer); } if (!success) { if (compr_buffer->size() > 0) { compr_buffer->pop_back(); } } } else { if (node->get_letter() == search_node) { success = true; } else { if (compr_buffer->size() > 0) { compr_buffer->pop_back(); } success = false; } } return success; } |
Aus dem intuitiven Ansatz habe ich zur Präsentation die Kompression einfacher Strings ausgelassen (mit … gekennzeichnet), um das Vorhaben übersichtlich zu gestalten:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | bool* Huffman::compress(bool* compr_bits_ar, int* count, string text, bool file) { vector compr_bits; vector cur_compr_bits; vector letters; if (file) { read_file(text, &letters); for (unsigned int i = 0; i < letters.size(); i++) { cur_compr_bits.clear(); depth_search(letters[i], root, &cur_compr_bits); compr_bits.insert(compr_bits.end(), cur_compr_bits.begin(), cur_compr_bits.end()); print_status(letters.size(), i); } } else { //... } //... //Rausgenommen, da trivial: compr_bits umgekehrt an das Ende von compr_bits_ar anfügen *count = compr_bits.size(); return compr_bits_ar; } |
Folgt nun der tabellarische Algorithmus. Er arbeitet mit einer Lookup-Tabelle. Auf diese kann direkt zugegriffen werden, da die Positionen bekannt sind (Position = Dezimalwert des Zeichens). Dort ist nun vermerkt, an welcher Stelle das jeweilige Blatt zu finden ist. Dieses wird ausgewählt und von dort aus geht es dann zum Vorgänger-Knoten, solange bis man beim Root-Knoten angekommen ist. Hierbei wird nun in jedem Schritt notiert, ob das aktuelle Element ein linker oder ein rechter Nachfolger ist. Bei einem linken, wird eine 0 (false) notiert, bei einem rechten entsprechend eine 1 (true).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | /** Komprimiert einen Text/Datei mit Hilfe einer Tabelle. Er geht den Text Zeichen fuer Zeichen durch, sucht das Zeichen in einer Tabelle (Laufzeit O(n)) und geht von diesem gefundenen Element so lange zum Vorgaenger, bis er beim obersten Element (root) angekommen ist. Dabei wird jeweils das aktuelle Bit notiert. Gesamtlaufzeit O(n * log n). @param compr_bits_ar Zeiger auf Array, in das die Kompressions-Bits geschrieben werden sollen @param count Zeiger auf Zahl, in die die Anzahl der Kompressions-Bits geschrieben werden soll @param text zu komprimierender Text/Datei @param file 0, wenn Text, sonst Datei @returns Zeiger auf neuen Speicherbereich, in den die Kompressions-Bits geschrieben wurden */ bool* Huffman::compress_table(bool* compr_bits_ar, int* count, string text, bool file) { vectorletters; unsigned int index = 0; bool* compr_bits_rev = new bool[tree[0]->get_longest_code()]; int lookup_position_index = 0; if (file) { read_file(text, &letters); compr_bits_ar = new bool[tree[0]->get_longest_code() * letters.size()]; for (unsigned int i = 0; i < letters.size(); i++) { lookup_position_index = lookup_positions[(int)letters[i]]; if (lookup_position_index >= 0 && lookup_position_index |
Wie zu sehen ist, wird eine „insert_compr_bits“ Methode verwendet, die hier zu sehen ist:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | /** Hilfsfunktion fuer die Tabellen-Kompression. Geht solange zum Vorgaenger, bis das root-Element erreicht ist und schreibt jeweils den Pfad (linkes oder rechtes Element) an das Ende des Bit-Arrays. @param compr_bits Bit-Array, in das geschrieben werden soll @param compr_bits_index aktueller Index, ab dem geschrieben werden kann @param compr_bits_rev Bit-Array zum Umdrehen des Codes @param cur_element Element, fuer das der Bitstream gesucht und geschrieben werden soll @returns naechste freie Position des Bit-Arrays */ int Huffman::insert_compr_bits(bool* compr_bits, unsigned int compr_bits_index, bool* compr_bits_rev, HuffmanElement* cur_element) const { int index = 0; while (cur_element != root) { compr_bits_rev[index] = cur_element->get_is_right(); ++index; cur_element = cur_element->get_parent(); } for (int i = index - 1; i >= 0; i--) { compr_bits[compr_bits_index] = compr_bits_rev[i]; ++compr_bits_index; } return compr_bits_index; } |
An dieser Stelle werden also die Auswertungen der Nachfolger vollzogen und an die Kompressions-Bits angehängt.
Dieser Algorithmus ist schon um Längen schneller als der erste. Aber zur genaueren Auswertung will ich später kommen.
Zunächst stelle ich noch die letzte und effizienteste der 3 Versionen vor:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | /** Komprimiert einen Text/Datei mit einer Tabelle und einer weiteren Lookup-Tabelle Er geht den Text Zeichen fuer Zeichen durch, sucht das Zeichen in einer Tabelle (Laufzeit O(n)). In diesem Zeichen ist der korrekte Bit-Stream gespeichert, der nur noch an den kompletten Bitstream angefuegt werden muss. Gesamtlaufzeit O(n) -> linear. @param compr_bits_ar Zeiger auf Array, in das die Kompressions-Bits geschrieben werden sollen @param count Zeiger auf Zahl, in die die Anzahl der Kompressions-Bits geschrieben werden soll @param text zu komprimierender Text/Datei @param file 0, wenn Text, sonst Datei @returns Zeiger auf neuen Speicherbereich, in den die Kompressions-Bits geschrieben wurden */ bool* Huffman::compress_lookup(bool* compr_bits_ar, int* count, string text, bool file) { bool* cur_compr_bits; HuffmanElement* current_element = 0; vector letters; unsigned int position = 0; int lookup_position_index = 0; if (file) { read_file(text, &letters); compr_bits_ar = new bool[tree[0]->get_longest_code() * letters.size()]; for (unsigned int i = 0; i < letters.size(); i++) { lookup_position_index = lookup_positions[(int)letters[i]]; if (lookup_position_index >= 0 && lookup_position_index get_lookup_code(); for(int j = (current_element->get_lookup_code_length()-1); j >= 0; j--) { compr_bits_ar[position] = cur_compr_bits[j]; ++position; } } } } else { //... } *count = position; return compr_bits_ar; } |
Dieser Code arbeitet ähnlich dem vorherigen. Der Unterschied ist nur, dass wir nicht mehr zurück zu den Vorgängern gehen, sondern mit dem bei der Erstellung des Baumes gespeicherten Lookup-Codes arbeiten. Somit ersparen wir uns die ständigen Wege zum Root-Element.
Der letzte Code-Ausschnitt, den ich vorstellen will, ist der der Dekompression:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | /** Dekomprimiert ein uebergebenes Bit-Array und speichert den dekomprimierten Text bei Bedarf in einer Datei @param compr_bits Kompressions-Bit-Array @param count Laenge des Kompressions-Bit-Arrays @param filename wenn Dateiname leer, dann wird der Text zurueckgegeben und nicht gespeichert, sonst wird er gespeichert @returns dekomprimierter Text, wenn er nicht gespeichert werden sollte, sonst leer */ string Huffman::decompress(bool* compr_bits, int count, string filename) { clock_t time_start = clock(); stringstream decompr_string; HuffmanElement* node; int i = 0; while (i < count) { node = root; while (i < count && (node->get_left() != 0 || node->get_right() != 0)) { if (!compr_bits[i]) { if (node->get_left() != 0) { node = node->get_left(); } } else { if (node->get_right() != 0) { node = node->get_right(); } } i++; //print_status(count, i); } decompr_string << node->get_letter(); } if (filename != "") { ofstream file; file.open(filename); file << decompr_string.str(); file.close(); decompr_string.str(""); } cout << endl << "Dauer: " << ((double)(clock() - time_start)) / 1000.0 << " Sekunden" << endl << endl; return decompr_string.str(); } |
Es werden alle Bits des Bitstreams (in dem Fall ein boolsches Array) durchgelaufen. Wobei beim Root-Element begonnen wird. Bei einer gelesenen 0, wird der linke Nachfolger als aktuelles Element festgelegt, bei einer gelesenen 1 der rechte Nachfolger. Sobald das aktuelle Element keinen Nachfolger mehr besitzt, ist es ein Blatt und der Buchstabe wird gespeichert. Im gleichen Schritt wird auch das aktuelle Element wieder auf den Root-Knoten festgesetzt.
Laufzeitanalyse
Die Komplexität der Dekompression liegt in O(n * log n), da jedes Bit durchlaufen wird und für jeden dieser Schritte sich der Baum halbiert.
Die Komplexität des intuitiven Algorithmus ist recht schlecht, sie liegt in O(n2). Dies kommt zu Stande, da die Tiefensuche eine Laufzeit von O(Knoten + Kanten) beträgt und diese für jedes Element durchgeführt werden muss.
Dies behebt die Tabellen-Variante. Deren Laufzeit liegt in O(n * log n): Für jedes (direkt zugreifbares) Blatt, muss der Baum nach oben durchlaufen werden.
Mit dem 3. Algorithmus sollte es mir gelungen sein, eine lineare und somit optimale Laufzeit zu erhalten. Für jeden Buchstaben muss nur ein Zugriff geschehen. Das Element steht fest und auch der Code von diesem ist direkt abrufbar. Er liegt also in O(n).
Soweit zu der theoretischen Komplexität.
Im Laufe meiner Programmierung des Huffman-Codes testete ich allerdings auch noch einige Datentypen.
Ich begann mit Vektoren und Listen, um die einzelnen Bits und Buchstaben zu speichern. Daher sind davon auch noch einige wenige Elemente im Code vorzufinden. Wie zu erwarten war, sind diese aber extrem langsam. Daher stellte ich das ganze auf Arrays um, für die ich die maximalen notwendigen Speicherbereiche reservierte, um keine weiteren Speicherstellen dynamisch anlegen zu müssen (wäre sonst ein großer Zeitverlust).
Allein diese Umstellung konnte den intuitiven und gleichzeitig langsamsten Algorithmus auf meinem Rechner bei einer Dateigröße von 1 MB von über 50 Sekunden auf 10 Sekunden senken.
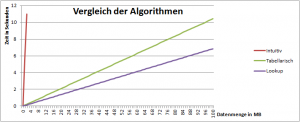
Um diesen Gedanken abzuschließen, möchte ich als letztes eine Grafik präsentieren, die die verschiedenen Laufzeiten (Durchschnitts-Tests) vergleicht:
Wir sehen also, dass die stärksten Unterschiede vom intuitiven zu den anderen Algorithmen zu sehen sind. Aber auch zwischen den beiden tabellarischen sind starke Unterschiede zu erkennen. Es lohnt sich also, bei der Binär-Baum Erstellung etwas mehr Zeit zu investieren, um die notwendigen Daten (Vorgänger etc.) zu ermitteln, da diese Erstellung nur ein Mal geschieht.
Das ganze habe ich kompiliert und für euch zum Testen hochgeladen: Der Download ist über das Download-Center möglich.
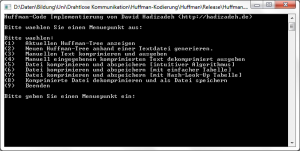
Screenshot des Tools:
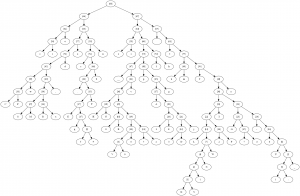
Beispiel-Binär-Baum:
Ich hoffe, ich konnte euch dieses, für mich sehr interessante Thema, etwas näher bringen und euch Ansätze und Ideen für die Huffman-Code-Implementierung geben.
Kategorie: News, Programmierung |
Schlagwörter: cpp, huffman, kompression, string-kompression